meta data for this page
This is an old revision of the document!
Temperatursensoren
AD590
Der AD590 ist eine integrierte Schaltung, die unabhängig von der Versorgungsspannung einen Strom fließen lässt, der proportional zu seiner lokalen Temperatur ist. Die Schaltung ist so kalibriert, dass der Strom in µA gerade die Temperatur in Kelvin angibt.
Der Messbereich des Sensors liegt zwischen -55 °C und 150 °C. Die absolute Genauigkeit ohne Kalibrierung wird zwar mit nur +/- 5 K angegeben. Die Wiederholbarkeit und die Langzeitdrift werden jedoch als kleiner als 0.1 K garantiert.
Das Preisschild für den AD590 liegt bei etwa 10 €. In der Version für höhere Genauigkeit, kostet er noch deutlich mehr.
NTC-Widerstand
| Temp. (°C) | Pt100 (Ω) | Pt1000 (Ω) | NTC-10k (Ω) |
|---|---|---|---|
| -200 | 18.5 | 185 | |
| -195 | 20.7 | 207 | |
| -194 | 21.1 | 211 | |
| -190 | 22.8 | 228 | |
| -185 | 25.0 | 250 | |
| -180 | 27.1 | 271 | |
| -175 | 29.2 | 292 | |
| -170 | 31.3 | 313 | |
| -165 | 33.4 | 334 | |
| -160 | 35.5 | 355 | |
| -155 | 37.6 | 376 | |
| -150 | 39.7 | 397 | |
| -145 | 41.7 | 417 | |
| -140 | 43.8 | 438 | |
| -135 | 45.9 | 459 | |
| -130 | 47.9 | 479 | |
| -125 | 50.0 | 500 | |
| -120 | 52.0 | 520 | |
| -115 | 54.1 | 541 | |
| -110 | 56.1 | 561 | |
| -105 | 58.2 | 582 | |
| -100 | 60.2 | 602 | |
| -95 | 62.2 | 622 | |
| -90 | 64.3 | 643 | |
| -85 | 66.3 | 663 | |
| -80 | 68.3 | 683 | |
| -75 | 70.3 | 703 | 8.5e6 |
| -70 | 72.3 | 723 | 5.2e6 |
| -65 | 74.3 | 743 | 3.2e6 |
| -60 | 76.3 | 763 | 2.1e6 |
| -55 | 78.3 | 783 | 1.3e6 |
| -50 | 80.3 | 803 | 896e3 |
| -45 | 82,29 | 822,9 | 606e3 |
| -40 | 84,27 | 842,7 | 416e3 |
| -35 | 86,25 | 862,5 | 291e3 |
| -30 | 88,22 | 882,2 | 206e3 |
| -25 | 90,19 | 901,9 | 148e3 |
| -20 | 92,16 | 921,6 | 108e3 |
| -15 | 94,12 | 941,2 | 79.5e3 |
| -10 | 96,09 | 960,9 | 59.2e3 |
| -5 | 98,04 | 980,4 | 44.7e3 |
| 0 | 100,00 | 1000,0 | 34.0e3 |
| 5 | 101,95 | 1019,5 | 26.2e3 |
| 10 | 103,90 | 1039,0 | 20.3e3 |
| 15 | 105,85 | 1058,5 | 15.9e3 |
| 20 | 107,79 | 1077,9 | 12.6e3 |
| 25 | 109,73 | 1097,3 | 10.0e3 |
| 30 | 111,67 | 1116,7 | 8.02e3 |
| 35 | 113,61 | 1136,1 | 6.48e3 |
| 40 | 115,54 | 1155,4 | 5.27e3 |
| 45 | 117,47 | 1174,7 | 4.31e3 |
| 50 | 119,40 | 1194,0 | 3.55e3 |
| 55 | 121,32 | 1213,2 | 2.94e3 |
| 60 | 123,24 | 1232,4 | 2.45e3 |
| 65 | 125,16 | 1251,6 | 2.06e3 |
| 70 | 127,07 | 1270,7 | 1.73e6 |
| 75 | 128,98 | 1289,8 | 1.46e3 |
| 80 | 130,89 | 1308,9 | 1.25e3 |
| 85 | 132,80 | 1328,0 | 1.06e3 |
| 90 | 134,70 | 1347,0 | 913 |
| 95 | 136,60 | 1366,0 | 786 |
| 100 | 138,50 | 1385,0 | 680 |
| 105 | 140,39 | 1403,9 | 590 |
| 110 | 142,29 | 1422,9 | 450 |
| 150 | 157,31 | 1573,1 | 192 |
| 200 | 175,84 | 1758,4 | 71 |
Wertetabelle für PT100, PT1000 und den 10k-NTC B57861S
Das Kürzel “NTC” steht für Negative Temperature Coefficient. Im Gegensatz zu dem meisten anderen Materialien nimmt bei ihnen der elektrische Widerstand mit steigender Temperatur ab. Typischerweise bestehen sie aus einem Halbleiter, bei dem sich mit steigender Temperatur immer mehr Elektronen im Leitungsband aufhalten.
Der große Vorteil von NTC-Widerständen liegt im starken Zusammenhang zwischen Temperatur und Widerstand. Dadurch ist es ohne großen Aufwand möglich Temperaturschwankungen im Bereich von mK zu messen. Dabei ist zu beachten, dass dies keine absolute Genauigkeit darstellt. Über lange Zeiträume von einigen Wochen und Monaten hinweg macht der Widerstand von NTCs eine Drift durch Alterung durch. Der genaue Betrag ist abhängig vom Typ und der Temperatur, bei der er gelagert wird. Er liegt unter ungünstigen Umständen im einstelligen Prozentbereich. Für den EPCOS B57861S ist die Drift in 10000 Stunden unter 70°C im mit kleiner als 2% spezifiziert.
Der Widerstand eines NTC hängt exponentiell vom Kehrwert der Temperatur ab:
<latex>R(T) = R_r \, \exp( \beta (1/T -1/T_r))</latex>
wobei <latex>R_r</latex> der nominelle Widerstand bei der Temperatur <latex>Tr</latex> und <latex>\beta</latex> ein vom Typ abhängiger Parameter ist.
Der 10k NTC von EPCOS, Typ B57861S103F40 hat
<latex>\beta=3988</latex>
Die Formel passend für das calc-Tool:
Rr=10000; Tr=273.15+25; T=273.15+26; b=3988; exp(b*(1/T -1/Tr))*Rr
Faustregel für einen 10k-NTC bei Raumtemperatur: 440 Ohm/K, oder 4.4% pro Kelvin. Das entspricht einem Temperaturkoeffizienter von 4.4e4 ppm/K Bei einer Messbrücke über 10V und einer 1:1 Differenz-Verstärkung macht das 10 mV/K, oder auch 10 µV/mK. Das ist viel im Vergleich zu dem Signal, dass man von einem PT100 oder erwarten kann. Dennoch bedeutet es, dass im Regelkreis eine große Verstärkung nötig ist und eine Messung von mK anfällig gegen elektromagnetische Einstreuungen ist.
Mehr und vor allem allgemeine Info gibts bei Wikipedia
PT100 / PT1000
Ein PT100 oder PT1000 Temperatursensor besteht im wesentlichen aus einem dünnen Platindraht. Dessen Widerstand ändert sich halbwegs linear mit der Temperatur. Die Drift durch Alterung, oder Umwelteinflüsse ist sehr klein. Ein Messung des Widerstands lässt sich daher ohne große Kalibrierung und mit guter absoluter Genauigkeit in einen Temperatur-Wert umsetzen.
Der Nachteil von Platin-Widerständen ist der im Vergleich zum NTC-Widerstand kleine Temperatur-Koeffizient. Das erschwert eine Messung mit hoher Auflösung. Typischerweise wird die Genauigkeit durch Rauschen und Drift der den Widerstand messenden Analog-Elektronik bestimmt. Außerdem trägt der Widerstand der Zuleitungen und ihr Temperaturkoeffizient zur Messung bei. Ein anderes Problem ist die Heizung des Platin-Widerstands durch den für die Messung fließenden Strom. Thermometer auf Basis von PT100 arbeiten daher häufig im Puls-Betrieb, um den Wärmeeintrag durch die Messung klein zu halten.
Pro Kelvin ändert sich der Widerstand um etwa 3.5e-3, also 3500 ppm/K. Faustregel für PT 100 ist damit 0.35 Ω/K.
Digitaler Temperatursensor DS18B20
Der DS18B20 ist ein Temperatursensor, dessen Wert digital ausgelesen werden kann. Ein integrierter (sehr kleiner) Mikroprozessor sorgt für die Linearisierung und die Kommunikation über ein serielles Protokoll. Das heißt, dieser Baustein kann direkt an einen Mikrocontroller angeschlossen werden.
Die absolute Genauigkeit dieses Sensors liegt bei etwa 0.5 K. Je nach programmierbarer Konfiguration entspricht die Höhe der Stufen zwischen zwei benachbarten digitalen Werten einem Temperaturunterschied zwischen 0.5 K und 0.06 K.
Thermoelemente
Thermoelemente nutzen den Seebeck-Effekt bei einem Stromkreis mit Leitungen aus unterschiedlichem Metallen. Dabei tritt eine Spannung auf, die proportional zum Temperatur-Unterschied zwischen den Kontaktstellen der Metalle ist. Diese Spannung beträgt zwar nur einige mV pro Kelvin. Dafür steigt sie über einen großen Temperaturbereich in guter Näherung linear an.
Die Proportionalitätskonstante zwischen Seebeck-Spannung und Temperaturunterschied hängt von der Wahl der Metalle ab. Bestimmte Paarungen mit besonders günstigen elektrischen, oder mechanischen Eigenschaften werden mit einem Buchstaben benannt (“Typ K”, “Typ J”, “Typ E”, …) Siehe dazu auch diese Tabelle bei Wikipedia.
Der AD597 ist ein Verstärker, der speziell dafür entwickelt sind, die Seeebeckspannung eines Thermoelements vom Typ K in ein Signal zu verwandeln, der für weitere Anwendungen, wie etwa AD-Wandler geeignet sind. Dieser Baustein ist intern so abgeglichen, dass sein Ausgang eine Spannung 10 mV/K aufweist. Mit einer speziellen Beschaltung kann dieser Baustein auch direkt als Temperatursensor eingesetzt werden, ohne das ein Thermoelement angeschlossen ist.
Anbringung von Temperatursensoren
Bezüglich einer zu regelnden Temperatur bedeutet das: Der Temperatur-Sensor gehört so dicht wie möglich an das Peltier.
Vorwort
Immer wieder hört man aber Stimmen, die etwas gegensätzliches behaupten. Die aufgebrachten Argumente sind meistens von der Art “Aber ich will doch an Punkt XYZ eine stabile Temperatur haben und nicht am Peltier”. Dass man mit diesem Argument ein stabiles Regel- und somit Temperaturverhalten bekommt, ist leider ein weit verbreiteter Irrglaube. Dieser Abschnitt dient dazu, den Vorteil einer direkten Anbringung nahe des Peltiers näher zu erläutern.
Erklärung
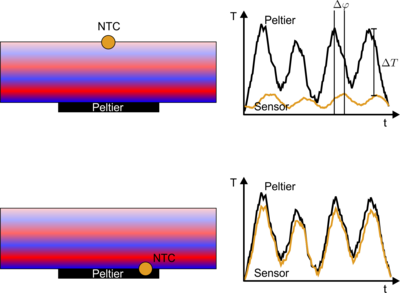
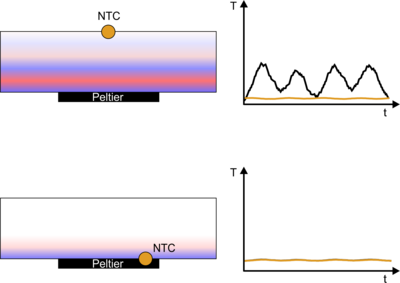
Nehmen wir einmal folgende Situation an. Ein Lasergehäuse soll Temperaturstabilisiert werden. Im ersten Fall ist der Sensor weit weg vom Peltier-Element angebracht. Strom- und somit Temperaturschwankungen am Peltier übertragen sich nun zum einen verzögert durch das Lasergehäuse (Phase-Lag) und sind zum anderen auf Grund der Trägheit von Temperaturprozessen auch stark gedämpft: Der Sensor nimmt nur einen einen Bruchteil der eigentlichen Schwankungen war. Anders sieht dies aus, wenn der Sensor sehr nahe am Peltier sitzt. Strom- und somit Temperaturschwankungen können hier nahezu unverfälscht gemessen werden.
Dies hat eine direkte Auswirkung auf die Regelung. Während im Falle eines weit entfernten Sensors das Sensorsignal “OK” aussieht, schwingt die Regelung potentiell unbemerkt auf und vermag externe Einflüsse nur langsam zu kompensieren.
Sitzt der Sensor allerdings am Peltier, kann die Regelung einem Überschwingen direkt entgegenwirken. Das restliche Gehäuse ist nun auf Grund des trägen Temperaturverhaltens passiv stabil. Generell erhält man mit dieser Methode ein deutlich stabileres Regel-Verhalten. Deshalb ist eine Anbingung des Sensors so dicht wie möglich an das Peltier-Element immer vorzuziehen.